对数函数的定义域及求解方法（了解对数函数的定义域及如何求解）

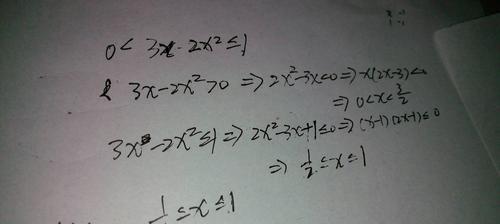
对数函数是一种常见的数学函数，广泛应用于科学和工程领域。在研究对数函数时，我们需要了解其定义域以及如何求解。本文将介绍对数函数的定义域的概念，并讨论求解方法，帮助读者更好地理解和应用对数函数。

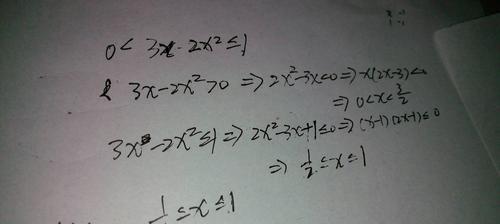
1.对数函数的基本定义

-对数函数是指以某个固定正实数为底数的指数函数，常用的底数有自然对数e和以10为底的常用对数。

-以e为底的自然对数函数被广泛应用于微积分和概率论等领域。

2.对数函数的定义域概念

-定义域是指一个函数能够取值的所有实数的。

-对于对数函数来说，定义域要求底数大于0且不等于1，因为这样才能保证对数的结果是实数。

3.以e为底的自然对数函数的定义域

-以e为底的自然对数函数的定义域是所有正实数，即x∈(0,+∞)。

-自然对数函数的图像在x轴的右侧无限延伸。

4.以10为底的常用对数函数的定义域

-以10为底的常用对数函数的定义域是所有正实数，即x∈(0,+∞)。

-常用对数函数的图像在x轴的右侧无限延伸。

5.对数函数的求解方法

-对于一般的对数函数，可以通过换底公式将其转换为以底数e或10为底的对数函数。

-换底公式为loga(x)=ln(x)/ln(a)，其中ln表示以e为底的自然对数。

6.对数函数定义域的示例

-示例一：求解log2(x)=3的定义域。根据定义域的要求，底数必须大于0且不等于1，所以x必须大于0。将方程转换为指数形式可得x=2^3=8，因此定义域为x∈(0,+∞)。

-示例二：求解ln(x+1)-2>0的定义域。移项并取指数形式可得x+1>e^2，因此定义域为x>e^2-1。

7.对数函数的常见性质

-对数函数具有一些常见的性质，如对数与指数的互逆性、对数函数的增减性等。

-这些性质在求解对数函数的定义域时可以发挥重要作用。

8.对数函数在实际问题中的应用

-对数函数在许多实际问题中起到关键作用，如对数模型的建立、指数增长和衰减问题等。

-了解对数函数的定义域和求解方法，有助于我们更好地应用对数函数解决实际问题。

9.求解对数函数定义域的注意事项

-在求解对数函数的定义域时，需要注意底数不能为0或1，否则对数结果将无意义。

-除此之外，还需考虑其他限制条件，如分母不能为0等。

10.对数函数与其他数学函数的关系

-对数函数与指数函数、幂函数等有着密切的关系，它们互为反函数。

-这种关系在解决复杂的数学问题时，往往能够简化计算过程。

11.对数函数在科学与工程领域中的应用举例

-对数函数在科学和工程领域中有着广泛的应用，如声音强度、震级、天文学中的星等级等。

-这些应用涉及到对数函数定义域的求解以及对数函数性质的应用。

12.对数函数的图像和特点

-对数函数在定义域内具有特殊的图像和特点，如在底数大于1时，函数图像呈现上升趋势；在底数小于1时，函数图像呈现下降趋势。

-了解这些特点有助于我们对对数函数进行更深入的理解。

13.对数函数求解方法的比较与选择

-在求解对数函数的定义域时，有多种方法可供选择，如换底公式、指数形式转化等。

-根据具体问题的需要，选择合适的方法进行求解。

14.对数函数定义域与求解方法的综合应用

-将对数函数定义域的求解方法与具体问题相结合，进行综合应用。

-通过实际问题的训练，提高对对数函数定义域求解方法的运用能力。

15.

-通过本文的介绍，我们了解了对数函数的定义域概念和求解方法，并掌握了应用对数函数解决实际问题的基本技巧。

-对数函数作为一种重要的数学工具，在科学和工程领域有着广泛的应用前景。